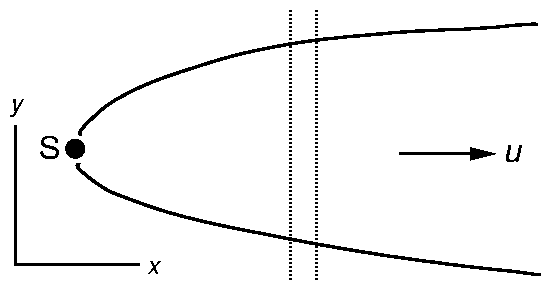
Fig. 8. A plan view of a plume of pollutant from a continuous point source S.
Fig. 8. A plan view of a plume of pollutant from a continuous point source S.
Consider a slice of air 1 m thick moving in the ![]() -direction, extending
to infinity in the
-direction, extending
to infinity in the ![]() and
and ![]() directions and moving with the mean wind
directions and moving with the mean wind ![]() .
The time taken for the slice to pass a fixed point is
.
The time taken for the slice to pass a fixed point is ![]() seconds. If the
source emits
seconds. If the
source emits ![]() kgs
kgs![]() of pollutant, then the amount in the slice is
of pollutant, then the amount in the slice is
![]() .
The pollutant diffuses in the
.
The pollutant diffuses in the ![]() ,
, ![]() and
and ![]() directions. But since
the source is continuous, about the same amount of pollutant diffuses into
the sheet in the
directions. But since
the source is continuous, about the same amount of pollutant diffuses into
the sheet in the ![]() -direction as diffuses out through the opposite side.
Diffusion in the
-direction as diffuses out through the opposite side.
Diffusion in the ![]() -direction therefore has negligible effect. The diffusion
problem reduces to that of 2-dimensional diffusion in the
-direction therefore has negligible effect. The diffusion
problem reduces to that of 2-dimensional diffusion in the ![]() ,
, ![]() plane but
in a frame of reference moving in the
plane but
in a frame of reference moving in the ![]() -direction with speed
-direction with speed ![]() . The
2-dimensional diffusion solution Eq. (22) therefore applies, but with
. The
2-dimensional diffusion solution Eq. (22) therefore applies, but with ![]() .
In other words
.
In other words